Prepočet priemeru vrtule pri zmene počtu listov

[igorb]

Možno by bolo dobré si zadefinovať, či hovoríme obecne o vrtuliach, alebo o vrtuliach na nejaké konkrétne použitie.

Pretože v súčasnosti dosť "frčia" koptéry či dokonca konvertoplány a tam by som pri statickom ťahu o nulovej účinnosti radšej nehovoril .

zda sa ze modelari maju talent redefinovat zname a zauzivane terminy (kauza BLDC :- )) ), nastastie co je ucinnost vieme celkom dobre uz nejakych 200 rokov od dob Jamesa Watta, takze nie, nepotrebujeme redefinovat co je ucinnost, lepsie je vynalozit trochu usilia na jej pochopenie :- ))) ... fakt to neboli ... a kto ma opacny nazor, odporucal by som prejs si knihu fyziky pre ZS

nebude asi potreba prilis intelektualneho usilia pochopit co som tam vyssie povedal okolo ucinnosti a vrtul, su to zame faky, neverit im ktokolvek moze, ale nic na tom nezmeni :- )))) :

1/ vrtula s vysokym P/D ( 1 a kusok viac - ta cervena) ma lepsiu ucinnost (pre rypakov - samozrejme sa tym mysli maximalna, nie ta v statickom rezime ktora je 0lova ani nejaka ina, ktora moze kludne hocijaka nizsia) ako tie s mensim stupanim, trebars v rozsahu 0,5 az 1 ... zelena, modra
2/ vrtula v statickom rezime ma ucinnost =0 uplne vlavo na grafe a je jedno ako vyzera

[Atto]

Ja sa teda potupne priznávam, že som ZŠ absolvoval len-tak-tak a aj to, že som rypák, takže aby som nedostal na rypák, tak sa pýtam, čo to je V/(ND) - na zvislej osi?

[igorb]

Ja osobne vidim na zvislej osi ucinnost.

[igorb]

a ak si myslel horizontalnu os tak toto:

https://en.wikipedia.org/wiki/Advance_ratio

[Atto]

Prepáč, prepáč, to ten zhubný vplyv alkoholu na ľudský mozog.

Mal som na mysli vodorovnú os.

[igorb]

Ber to zjednodusene a uplne drevorubacsky ako doprednu rychlost.

[Atto]

a ak si myslel horizontalnu os tak toto:
https://en.wikipedia.org/wiki/Advance_ratio

No to si mi pomohol. Veď som písal, že ZŠ som absolvoval len-tak-tak a zabudol som dodať, že väčšinu času, obzvlášť hodiny angličtiny som strávil fajčením na záchode.

Ale tvoje vysvetlenie:

Ber to zjednodusene a uplne drevorubacsky ako doprednu rychlost.

už som schopný aspoň okrajovo pobrať.

Horšie je, že na tom grafe vidím, že pre V/(ND) menšie ako približne 0,49 to vyzerá lepšie pre vrtule s menším pomerom stúpania k ich priemeru.
Prepáč mi moje priblblé otázky, ale znamená to teda, že keď mám modely, ktoré lietajú skôr pomaly ako rýchlo, tak tie podštvorcové vrtule budú efektívnejšie ako štvorcové?

[VTjr]

... tym ze zmenis priemer a zachovas stupanie, zmeni sa ti P/D a s tym charakter vrtule ... ak zmenis stupanie, aby si zahoval P/D bude fungovat na inych otackach a potom ten vztah uz ale neplati ...

Tak potom nie 4. ale 5. odmocnina a ten vzorec by možno bolo lepšie upraviť nasledovne:

D/D2 = (2/n)^0,20 = P/P2

Kde:
D2 je známy priemer a P2 známe stúpanie 2-listej vrtule,
n je počet listov ekvivalentnej vrtule,
D je jej výsledný priemer a P stúpanie n-listej vrtule.

Vlastne by sa nejednalo o vzorec len pre priemer, ale pre koeficient geometrického zmenšenia vrtule (teda priemeru aj stúpania - pomer P/D sa teda zachováva) a tam, ako vieme, je závislosť umerná 5. mocnine koeficientu.

Edit:
Ale Igor, máš pravdu v tom, že tak či onak to bude iná vrtuľa a nikdy to nemôže byť presne prepočítateľné. Lebo ak by sme aj prepočítavali tak priemer ako aj stúpanie, menili súčasne obe hodnoty aby sme zachovali pomer P/D, tak sa aj tak pravdepodobne dostaneme do situácie, keď nám vyjdu dosť neštandartné rozmery, ktoré sa jednoducho nevyrábajú, ktoré nezoženieme, a aj tak budeme musiet zobrať niečo s blízkymi, ale trochu inými parametrami. A potom samozrejme bude všetko inak. A to už vôbec nehovorím o tom, že vrtuľa s iným počtom listov môže mať inú štíhlosť a tvar tých listov.

Preto treba tak tento upravený vzorec, ako aj ten čo som zverejnil na začiatku vlákna, brať len ako približný prepočet, aby sme sa vedeli od čohosi odpichnúť pri experimentálnom overení, teda aby sme nenamontovali na os motora niečo, čo bude úplne kdesi mimo.

[VTjr]

igorb: tym nedosiahnes vecsiu ucinnost, prave naopak, iba vecsi staticky tah, vecsiu ucinnost dostanes naopak pri tom stvorcovom stupani

Tak s týmto by som si dovolil, možno trochu trúfalo, nesúhlasiť:

Igor sa Ti to snažil vysvetliť na grafe, ja sa Ti to pokúsim vysvetliť slovne.

Ak ovšem účinnosťou elektropohonu rozumieme niečo ako pomer ťahu vrtule a príkonu elektropohonu.

Nie si prvý ani posledný, s takými sa stretávam často, čo toto nechápu.
V prvom rade, účinnosť je bezrozmerné číslo pomeru výkonu a príkonu (oboje je v kW). Nemôžeš teda dávať do pomeru ťah (teda silu v N) a príkon (v kW) - tým totiž dostaneš niečo iné, len nie účinnosť.
Teraz si zadefinujme čo vlastne požadujeme od vrtule, teda aký výkon? Chceme predsa, aby sa hmotné teleso (model), silou ťahu vrtule presunul o nejakú vzdialenosť a za nejaký čas! Ak sila ťahu vrtule 1N posunie model o dráhu 1m, tak sa vykoná práca 1J a ak sa to stihne za 1s, potom vrtuľa podala výkon 1W. Ale Príkon je to, čo musel dodať motor na hradeli tejto vrtule, aby sa to mohlo udiať.
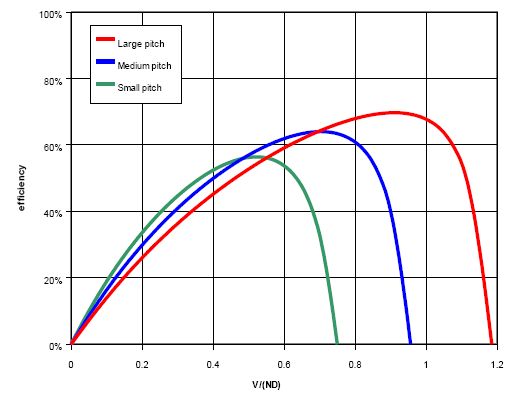
Ak motor beží, ale model sa nehýbe, tak dráha je = 0 a teda práca aj výkon sú nulové. To však neznamená, že motor nepodáva žiadny výkon. Naopak, ten môže byť značný, ale celý sa len jalovo spotrebuje na vírenie vzduchu okolo vrtule.

tak sa pýtam, čo to je V/(ND) - na zvislej osi?

Igor povedal, že sa jedná vlastne o rýchlosť.
Dosť to zjednodušil, lebo je to pravda len čiastočne, pretože V/(ND) rozmerovo nie je rýchlosť, ale je to zase bezrozmerné číslo vyjadrujúce pomer rýchlostí. Teda V - doprednej rýchlosti pohybu a n*D, čo je trochu ťažšie predstaviteľná hodnota, pretože n sú otáčky za sekundu, teda prevrátená hodnota času jednej otáčky a D je priemer vrtule, takže je to fakticky akási rýchlosť presunu o jeden preimer vrtule za dobu jednej otáčky. Tento pomer vyjadruje to, v akom pomere je rýchlosť (daná priemerom a otáčkami) k skutočnej rýchlosti dopredného pohybu. Ak sú otáčky alebo priemer malé a rýchlosť pohybu veľká, tak ten pomer rasitie, ak naopak je rýchlosť malá pri veľkom priemere alebo otáčkach, tak ten pomer klesá. V Igorovom grafe vidno, že je tam vždy isté maximum, a to je práve vtedy, keď je rýchlosť pohybu pri danom priemere a otáčkach taká, že je uhol nábehu listov optimálny (teda zjednodušene povedzme, že profily listov pracujú v režime maximálnej kĺzavosti, teda pomeru Cy/Cx, tada naväčšieho vztlaku pri dostatočne malom odpore). Treba si všimnúť, že vrtule s malým stúpaním majú toto maximum viac vľavo a tie s vyšším viac vpravo, teda pri vyšších rýchlostiach letu. A z toho vyplýva aj to, prečo bude menej stúpavá vrtuľa výhodnejšia pre malé rýchlosti alebo visenie a prečo štvorcová zas pri vyšších rýchlostiach letu, ale jej statický ťah bude nízky.

Ten pomer fakticky ilustruje to, pod akým uhlom nábehu budú obtekané listy vrtule. No a účinnosť vrtule sa mení práve v závislosti od toho aký je v danej situácii ten pomer. Ak bude dopredná rýchlosť malá, uhol nábehu listov bude veľký, a to bude znamenať vysoký ťah, ten bude s rýchlosťou síce postupne klesať, ale vďaka rýchlosti pohyby výkon poraste až do určitého maxima, kým nezačne byť uhol nábehu listov taký malý, že ťah vrtule začne prudko klesať. A to až do bodu nulového uhlu nábehu. Poprekročení tejto rýchlosti už bude uhol nábehu záporný a vrtuľa začne brzdiť, lebo listy budú vyvodzovať záporný ťah. A to, pri akej rýchlosti pohybu táto situácia nastane závisí jednak od stúpania, priemeru, ale hlavne od otáčok, znížením ktorých začneme brzdiť skôr a zvýšením naopak neskôr. Veľké lietadla majú možnosť meniť stúpanie listov, takže môžu ťah vrtule optimalizovať v širokom rozsahu aj bez zmeny otáčok.

[igorb]

Igor povedal, že sa jedná vlastne o rýchlosť. Dosť to zjednodušil, lebo je to pravda len čiastočne

Ano, ako som povedal je to velezjednodusene povedane ... zjednodusene presne tak, ze ak pouzijeme vrtule s rovnakymi priemermi pri rovnakych otackach, cize lisiacimi sa iba stupanim, potom na tej x osi mozem namiesto V/(nD) pisat iba to V cize rychlost a nic sa nezmeni

a zbytok uz plati presne ako pise VTjr cize zjednodusene ak mam vrtulu s malym stupanim (zelena) tak ta dosiahne vrchol svojej ucinnosti pri nizkych rychlostiach a ta s velkym stupanim (cervena) pri vyssej rychlosti ... co je dost pochopitelne a ocakavatelne, podstatou tej informacie o ktorej tu ide rec je ze ta cervena s vecsim stupanim dosiahne vyssie ako ta zelena (ale az vo vyssej rychlosti, pri tej nizsej je viditelne horsia), a to ze ten staticky rezim s tym nema nic spolocne, ucinnosti su tam nulove

[igorb]

A toto pisem oddelene aby bolo jasne ze tu ide o nieco ine - vysvetlenie preco je tam V/(nD) a nie V

no aby sme nedospeli k nazoru ze velke stupanie je lepsie pri rychlejsom modeli a male pri pomalom, to by sa asi hotlinoletci postavili na zadne, ze ich vertikolety vyuzivaju hlavne tah a splhaju pri tom nahor so stvorcovymi vrtulami

my mozeme mat vrtulu s velkym stupanim ktora sa bude tocit mensimi otackami ... to znamena ze obe vrtule dosiahnu to maximum pri rovnakej rychlosti, preto ze ta s vecsim stupanim sa proste toci pomalsie

no a kedze mame nizsie otacky, vyssiu ucinnost, tak prikon bude viditelne mensi pri tej vrtuli s velkym stupanim

to nam da prebytok vykonu (voci tej zelenej) ktory nam dovoli zvecsit priemer vrtule (D)

... sory ze som vam to zase rozhadzal ked to uz vyzeralo jasne :- ))))

ten rules ktory diktuje volbu vrtule je totiz iny, male stupanie pouzijem ked potrebujem zhruba rovnaky tah vo velkom rozsahu rychlosti (sportove, akrobaticke modely) stvorcovu ak potrebujem vydojit posledne zbytky vykonu v relativne uzkom rozsahu rychlosti kde je model optimalizovany.

[VTjr]

...to by sa asi holinoletci postavili na zadne, ze ich vertikolety vyuzivaju hlavne tak a splhaju pri tom nahor so stvorcovymi vrtulami...

Tak ale u heliny hovoriť o stúpaní rotora je problematické, lebo rotory majú rovnaký uhol nábehu na celom liste, takže pri hlave je stúpanie malé a na koncoch iné, podstatne väčšie. Aj to je jedným z dôvodov, prečo sa roztočený rotor vyhne dohora, do tvaru obráteného dáždnika. U helin je lepšie hovoriť len o uhle nábehu. Samozrejme kvadro a iné koptéry majú vrtule s krútenými listami tak ako u letúňov-plošníkov (nepišem lietadiel, lebo aj koptéry aj letúne sú lietadlá), teda s konštantným stúpaním celého listu.

... sory ze som vam to zase rozhadzal ked to uz vyzeralo jasne :- ))))
...

Tak to sa Ti naozaj podarilo, lebo tomu už teraz pomaly nerozumiem ani ja. SKús to ešte raz rozviesť viac polopate.

Inak sám nerozumiem dosť dobre tomu, prečo v tom grafe o účinnosti na vodorovnú os udávajú pomerné číslo (Advance ratio) V/(nD) ? Prečo tam nie je skôr V/(nP) ? Mne tento pomer pripadá zrozumiteľnejší.
Každopádne pri ňom by každá vrtuľa mala nulovú účinosť pri hodnote V/(nP)=0 a aj pri =1 a medzitým by bol kdesi vrchol. Ale je pravda, že taký graf by neumožnil porovnanie vrtúľ s rôznym pomerom P/D. Možno som si týmto sám odpovedal.

[igorb]

Tak ale u heliny hovoriť o stúpaní rotora je problematické

sorry, precitaj si to este raz (opravil som preklepy), nehovoril som o helinach ale hotlineroch, to je typicky priklad ked sa vyuziva tah pri "relativne" nizkej rychlosti (ja viem ja viem, leti vam to nahor strasne rychlo ... ale vzdy pomalsie ako by to letelo dole :- ))) )

[VTjr]

Aha, čo dokáže malý preklep.
Teraz som už pochopil, čo si vlastne chcel povedať, to mi jasné je.

Ale čo ten môj posledný odstavec? Prečo tam nie je V/(nP)?

[igorb]

Ale čo ten môj posledný odstavec? Prečo tam nie je V/(nP)?

ak je dany graf o vrtuli s pevne danym P/D tak je to jedno nie? :- )))

zvykom je ale vzdy vsetko viazat na priemer